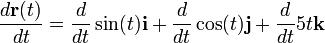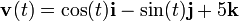jueves, 22 de octubre de 2009
Grupo: 2º de Bachillerato de Ciencias de la Naturaleza y la Salud, con 11 alumnos. Todos ellos casi sin haber manejado ordenadores en el centro, durante el Bachillerato, aunque alguno cursó la optativa Informática en la ESO y también hay alguno que tiene ordenador en casa y con Internet. Es un grupo considerado por el resto de los profesores como el mejor de los tres de 2º de Bachillerato. En matemáticas han tenido un rendimiento normal, pero con una actitud muy buena.
Objetivos:
Conocer y utilizar el concepto de vector en el espacio.
Aplicar el cálculo vectorial a la resolución de problemas geométricos.
Interpretar geométricamente cuestiones de dependencia e independencia lineal en el espacio.
Materiales
11 ordenadores conectados en red del aula de informática del Ciclo Formativo de Desarrollo de Aplicaciones Informáticas de nuestro Centro, cuyo uso fue posible al estar realizando la mayoría de los alumnos la Formación en Centros de Trabajo.
Tiempo:
Los días 23 y 24 de Abril en las horas de matemáticas.
Descripción del desarrollo
Con bastante antelación, encendí todos los ordenadores que iban a ser usados y comprobé que la red funcionaba; a continuación, grabé en uno de ellos la unidad didáctica, y fui creando en cada uno de los escritorios de los aparatos un acceso directo a la primera de las páginas; funcionaba. Sin embargo, cuando los alumnos llegaron, al acceder al mismo tiempo, se quejaban de que no salía nada. Un poco después, fue apareciendo en todos los monitores el índice de la unidad, con el consiguiente alivio por mi parte.
Antes de pasar a la primera escena, les comenté sobre la pizarra lo que iban a ver, y, para motivarles, les dije que lo que yo dibujaba lo verían mucho mejor en el ordenador.
A partir de ahí, desarrollamos todas las preguntas de la unidad, para lo que necesitamos dos clases.
En la mayoría de los casos, los alumnos sólo progresaban si yo explicaba lo que tenían que hacer, pero, cuando lo entendían, preferían la pantalla a la pizarra, cómo no. En particular, cuando llegamos a la última escena sobre el cambio de base, "decidimos" entre todos que sería mejor no intentar explicarlo geométricamente sobre la pizarra.
La actitud de los alumnos fue positiva en todo momento y lamentamos no poder tener más material.
Al ser una unidad de introducción a los vectores en el espacio, todos los alumnos asimilaron los conceptos geométricos correctamente, aunque el manejo algebraico todavía deja mucho que desear.
Valoración de la encuesta
La tabla siguiente recoge los valores medios de la encuesta que les pasé, y, en el caso de las preguntas de respuesta abierta, un resumen de lo que opinan:
Preguntas Media
1
¿Te gustan las matemáticas? (1-nada) y (5-mucho) 2,82
2
¿Qué nota sueles sacar en matemáticas? (1-insuficiente) y (5-sobresaliente) 2,45
3
¿Te interesó la experiencia cuando te la contaron? (1-nada) y (5-mucho) 4,00
4
¿Has tenido dificultades para hacer las actividades? (1-muchas) y (5-ninguna) 3,86
5
¿Prefieres este sistema al tradicional? (1-nada) y (5-totalmente) 3,77
6
¿Cuánto te parece que has aprendido? (1-nada) y (5-mucho) 3,82
7
¿Te ha gustado la experiencia? (1-nada) y (5-mucho) 4,45
8
¿Te ha gustado trabajar en equipo? (1-nada) y (5-mucho) 4,45
9
¿Te gustaría continuar trabajando con este método? (1-nada) y (5-mucho) 3,95
10
¿Crees que es posible aprender las matemáticas así? (1-nada) y (5-todo) 3,68
11. Indica qué es lo que más te ha gustado de esta experiencia:
Ver los conceptos mejor que en la pizarra y trabajar con los compañeros
12. Indica qué es lo que menos te ha gustado de esta experiencia:
No poder tomar apuntes porque eran difíciles, con lo que la teoría no queda clara, y la lentitud y baja calidad de los equipos y red
13. Indica lo qué cambiarías y lo que no cambiarías:
Seguir usando el ordenador para los ejemplos y dar la teoría como en clase
14. Si quieres aclarar algunas de las respuestas dadas en la tabla anterior escríbelo aquí:
Ninguna respuesta
15. Expresa tu valoración general o los comentarios que creas que son de interés:
Experiencia positiva, pues se entienden mejor los conceptos, pero que debe ser completada con el libro
Valoración personal
Espero poder ir completando las unidades sobre geometría del espacio, pues considero que es uno de los ámbitos donde puede ser más útil el uso del ordenador. Para mí ha sido una satisfacción poder por primera vez preparar unas clases que, aunque han supuesto un importante trabajo extra, son el punto de partida para hacer más asequible conceptos y resultados que, de la forma tradicional en la pizarra, siempre tenía la sensación de que bastantes alumnos no lo "veían".
No obstante, me pregunto: ¿cómo hubiera sido la experiencia de dar una clase con ordenadores si en lugar de 11 alumnos de 2º de Bachillerato hubieran sido 30 de 2º o 3º de ESO? El año próximo quizá me atreva a comprobarlo.
Sobre el proyecto Descartes en general, me gustaría que se resolvieran los problemas que pudiera haber para que se convirtiera en un "Manual Interactivo de Matemáticas para la Educación Secundaria" completo, que se pudiera después adaptar a cualquier situación educativa posible.
martes, 8 de septiembre de 2009
Problema Ilustratorio
El siguiente ejercicio es para aclarar el uso de vectores unitarios en este método analítico.
Un auto recorre 20 km hacia el Norte y después 35 km en una dirección 60º al Oeste del Norte. Determine magnitud y dirección del desplazamiento resultante del auto.
Hacemos un diagrama:
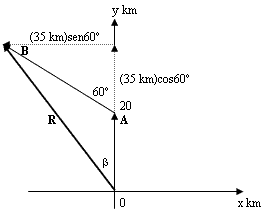
Expresando los dos desplazamientos componentes como A y B, indicados en la figura, y usando ![]() unitarios, tenemos:
unitarios, tenemos:
R = A + B. R es el vector resultante buscado, cuya magnitud se
denota ![]() y cuya dirección puede determinarse calculando el ángulo
y cuya dirección puede determinarse calculando el ángulo ![]() .
.
A = 20 km j, (apunta hacia el Norte).
B debemos descomponerlo en componentes x e y (ó i y j )
B = -(35 km)sen60ºi + (35 km)cos60ºj = -30.3 kmi + 17.5 kmj
Luego,
R = 20 kmj - 30.3 kmi + 17.5 kmj = 37.5j - 30.3i.
La magnitud se obtiene de
![]() 2 = (37.5km)2 + (30.3km)2
2 = (37.5km)2 + (30.3km)2 ![]()
![]() = 48.2 km
= 48.2 km
En el triángulo formado por cateto opuesto 30.3 y cateto adyacente 37.5, tg
Frecuentemente las cantidades vectoriales se expresan en términos de
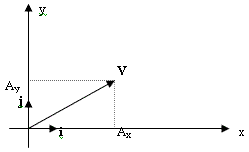
Ahora V puede escribirse
![]() V = Ax i + Ay j
V = Ax i + Ay j
Si necesitamos sumar el vector A = Ax i + Ay j con el vector
B = Bx i + By j escribimos
R = A + B = Ax i + Ay j + Bx i + By j = (Ax + Bx)i + (Ay + By)j
Las componentes de R (=A + B) son Rx = Ax + Bx y Ry = Ay + By
Clasificación de los mov. según las componentes at y an.
Atendiendo a estas componentes podemos decir que los movimientos rectos no tendrán aceleración normal ya que en ellos no se producen cambios en la dirección de la velocidad y los movimientos curvos tienen, al menos, aceleración normal ya que en estos necesariamente hay cambios en la dirección de la velocidad.
Dentro de los movimientos rectos podemos distinguir aquellos donde no se producen cambios en el módulo de la velocidad (at es nula) movimientos uniformes y aquellos donde si se producen cambios en el módulo de la velocidad...
Dentro de los movimientos curvos haremos especial hincapié en los movimientos circulares, radio de curvatura constante (R=cte.). También aquí podemos hablar de dos posibilidades, que at sea nula (módulo de la velocidad no varía -cte.-) o bien que at sea distinta de cero.

Estos son algunos de los movimientos que serán estudiados a lo largo del bloque.
Puede resultar conveniente expresar el arco de curva "s" en función del ángulo "theta" y el radio de curvatura con el que se traza dicho arco. Recordando la definición de radián...

Luego si el ángulo está expresado en radianes las relaciones entre las magnitudes lineales y las correspondientes angulares son las descritas arriba...
Definición
Habiendo definido el concepto de vector unitario al comienzo de este artículo y habiendo presentado la notación usual en la sección anterior, presentamos en esta sección una definición simbólica de vector unitario.
- Sea el vector v ∈ ℝn. Se dice que v es un vector unitario y se lo denota mediante
 si y solamente si |v| = 1.
si y solamente si |v| = 1.
O en forma más compacta:
Versor asociado a un vector
Con frecuencia es necesario contar con un vector unitario que tenga la misma dirección y sentido que un dado vector v. Es decir, se busca un vector con la misma dirección y sentido que un dado vector v, pero con (eventualmente) distinto módulo, y en particular, módulo unitario. A tal vector se lo llama versor asociado al vector v.
La operación vectorial que permite modificar el módulo de un vector sin alterar su dirección es el producto de escalar por vector. Buscamos entonces cual es el escalar k tal que, al multiplicarse por un vector v, da como resultado un vector de módulo unitario:
Por propiedad de módulo de un vector, podemos escribir:
Si aceptamos que v es un vector no nulo, podemos dividir ambos miembros de la ecuación por el módulo de v, es decir, por |v|, para obtener:
De esta manera:
El valor positivo corresponderá al factor que produce un vector unitario con el mismo sentido que el vector original v, mientras que el valor negativo producirá un vector unitario con sentido contrario a v.
De acuerdo con la definición de versor asociado a un vector dado (misma dirección y sentido, el versor asociado al vector v no nulo es:
Al proceso de obtener un versor asociado a un vector se lo llama normalización del vector, razón por la cual es común referirse a un vector unitario como vector normalizado.
El método para transformar una base ortogonal (obtenida, por ejemplo mediante el método de ortogonalización de Gram-Schmidt) en una base ortonormal (es decir, una base en la que todos los vectores son versores) consiste simplemente en normalizar todos los vectores de la base utilitando la ecuación anterior.
Producto escalar con vectores unitarios
En el espacio euclídeo, el producto escalar de dos vectores unitarios es simplemente el coseno del ángulo entre ellos. Esto es consecuencia de la definición de producto escalar y del hecho de que el módulo de ambos vectores es la unidad:
Pero:
Por lo tanto:
donde θ es el ángulo entre ambos vectores.
Proyección escalar
De lo anterior, resulta que el producto de un vector por un versor es la proyección escalar del vector sobre la dirección determinada por el versor.
Como el módulo del versor  es la unidad, la ecuación anterior se transforma en:
es la unidad, la ecuación anterior se transforma en:
de donde es evidente lo afirmado al comienzo de este apartado.
Este resultado es muy frecuente en física, donde en necesario operar, por ejemplo, con las componentes ortogonales a una superficie.
Vectores coordenados
En un sistema de coordenadas cartesianas, x, y y z los vectores unitarios o versores correspondientes a cada uno de los ejes se denotan por  , respectivamente. Estos versores se usan para expresar analíticamente los vectores por medio sus componentes. Por ejemplo, la expresión analítica del vector v = (1,-2,3) es:
, respectivamente. Estos versores se usan para expresar analíticamente los vectores por medio sus componentes. Por ejemplo, la expresión analítica del vector v = (1,-2,3) es:
sábado, 5 de septiembre de 2009
Representación gráfica
Se representa como un segmento orientado, con dirección y sentido, dibujado como una "flecha". Su longitud representa el modulo del vector y la "punta de flecha" indica su sentido.
Notación
Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flechita sobre la letra que designa su módulo (que es un escalar). Así, por ejemplo; 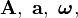 ... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector:
... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector: 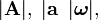 ...
...
Cuando convenga, representaremos la magnitud vectorial haciendo referencia al origen y al extremo del segmento orientado que la representa geométricamente; así, designaremos los vectores representados en la Figura 2 en la forma  , ... resultando muy útil esta notación para los vectores desplazamiento.
, ... resultando muy útil esta notación para los vectores desplazamiento.
Además de estas convenciones los vectores unitarios o versores, cuyo módulo es la unidad, se representan frecuentemente con un circunflejo encima, por ejemplo  .
.
Tipos de vectores
Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse distintos tipos de los mismos:
- Vectores libres: no están aplicados en ningún punto en particular.
- Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
- Vectores ligados: están aplicados en un punto en particular.
Podemos referirnos también a:
- Vectores concurrentes: sus rectas de acción concurren en un punto propio o impropio (paralelos)
- Vectores unitarios: vectores de módulo unidad.
- Vectores opuestos: vectores de distinto sentido, pero igual magnitud y dirección
- Vectores colineales: aquellos que comparten una misma recta de acción
Componentes de un vector
Un vector se puede expresar como una combinación lineal de tres de vectores unitarios o versores perpendiculares entre sí que constituyen una base vectorial.
En cordenadas cartesianas, los versores cartesianos se representan por 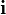 ,
, 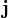 ,
, 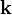 , correspondiendo a las direcciones de los ejes cartesianos x, y y z.
, correspondiendo a las direcciones de los ejes cartesianos x, y y z.
Expresión analítica
Las componentes del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:
o expresaese como una combinación de los versores definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será
Estas representaciones son equivalentes entre sí, y los valores ax, ay, az, son las componentes vector que, salvo que se indique lo contrario, son números reales.
Operaciones con vectores
Suma de vectores
Para sumar dos vectores libres vector y vector se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.
Método del paralelogramo
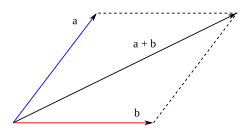
Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, completando un paralelogramo trazando rectas paralelas a cada uno de los vectores, en el extremo del otro (ver gráfico a la derecha). El resultado de la suma es la diagonal del paralelogramo que parte del origen común de ambos vectores.
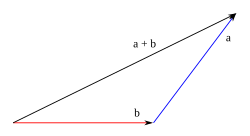
Método del triángulo
Consiste en disponer gráficamente un vector a continuación de otro; es decir, el origen de uno de los vectores se lleva sobre el extremo del otro. A continuación se une el origen del primer vector con el extremo del segundo.
Método analítico. Suma y diferencia de vectores [editar]
Dados dos vectores libres,
El resultado de su suma o de su diferencia se expresa en la forma
y ordenando las componentes,
Conocidos los módulos de dos vectores dados,  y
y  , así como el ángulo θ que forman entre sí, el módulo de
, así como el ángulo θ que forman entre sí, el módulo de  es:
es:
La deducción de esta expresión puede consultarse en deducción del módulo de la suma.
Producto de un vector por un escalar
El producto de un vector por un escalar es otro vector cuyo módulo es el producto del escalar por el módulo del vector, cuya dirección es la del vector original y cuyo sentido es el mismo u opuesto según que el escalar sea positivo o negativo.
Partiendo de la representación gráfica del vector, sobre la misma línea de su dirección tomamos tantas veces el módulo de vector como marque el escalar, que de ser negativo cambia el sentido (ver gráfico).
Partiendo de un escalar  y de un vector
y de un vector  , el producto de
, el producto de  por
por  se representa
se representa  y se realiza multiplicando cada una de las componentes del vector por el escalar; esto es, dado el vector
y se realiza multiplicando cada una de las componentes del vector por el escalar; esto es, dado el vector
su producto por el escalar  es
es
esto es, se multiplica por  cada una de las componentes del vector.
cada una de las componentes del vector.
Producto escalar
Producto vectorial
Derivada de un vector
Dado un vector que es función de una variable independiente
Calculamos la derivada del vector con respecto de la variable t, calculando la derivada de cada una de sus componentes como si de escalares se tratara:
 .
.
teniendo en cuenta que los versores son constantes en módulo, dirección, y sentido.
Veamos un ejemplo de derivación de un vector, partiendo de una función vectorial:
Esta función representa una curva helicoidal alrededor del eje z, de radio unidad, como se ilustra en la figura. Podemos imaginar que esta curva es la trayectoria de una partícula y la función  representa el vector de posición en función del tiempo t. Derivando tendremos:
representa el vector de posición en función del tiempo t. Derivando tendremos:
Realizando la derivada:
La derivada del vector de posición respecto al tiempo es la velocidad, así que esta segunda función determina el vector velocidad de la partícula en función del tiempo, podemos escribir:
Este vector velocidad es un vector tangente a la trayectoria en el punto ocupado por la partícula en cada instante. Si derivásemos de nuevo obtendríamos el vector aceleración.
Otras operaciones
Ángulo entre dos vectores
El ángulo determinado por las direcciones de dos vectores 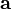 y
y  viene dado por
viene dado por
Requerimientos físicos de las magnitudes vectoriales
No cualquier n-tupla de funciones o números reales constituye un vector físico. Para que una n-tupla represente un vector físico, los valores numéricos de las componentes del mismo medidos por diferentes observadores deben transformarse de acuerdo con ciertas relaciones fijas.
En mecánica newtoniana generalmente se utilizan vectores genuinos, llamados a veces vectores polares, junto con pseudovectores, llamados vectores axiales que realmente representan el dual de Hodge de magnitudes tensoriales antisimétricas. El momento angular, el campo magnético y todas las magnitudes que en su definición usan el producto vectorial son en realidad pseudovectores newtonianos.
En teoría especial de la relatividad, por ejemplo, sólo los vectores tetradimensionales cuyas medidas tomadas por diferentes observadores pueden ser relacionadas mediante alguna transformación de Lorentz constituyen auténticas magnitudes vectoriales. Así las componentes de dos magnitudes vectoriales medidas por dos observadores 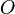 y
y  deben relacionarse de acuerdo con la siguiente relación:
deben relacionarse de acuerdo con la siguiente relación:
Donde  son las componentes de la matriz que da la transformación de Lorentz. Magnitudes como el momento angular, el campo eléctrico o el campo magnético o el de hecho en teoría de la relatividad no son magnitudes vectoriales sino tensoriales.
son las componentes de la matriz que da la transformación de Lorentz. Magnitudes como el momento angular, el campo eléctrico o el campo magnético o el de hecho en teoría de la relatividad no son magnitudes vectoriales sino tensoriales.